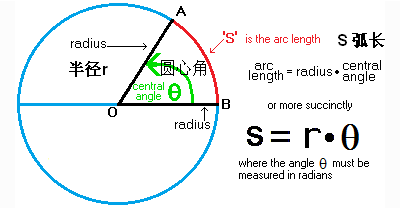
公式: S扇=(lR)/2 (l為扇形弧長) = (1/2)θR 2 (θ為以弧度表示的圓心角) 扇形面積 S扇=(n/360)πR 2 s扇=1/2lr(當知道弧長時) (n為圓心角的度數,R為扇形的半徑) 註:π為 圓周率 約等於 一般取314名前に「弧」とついているように,円の弧を使って定義します. 弧度法 半径1の扇形の弧の長さが θ であるとき,この扇形の中心角の大きさを θ rad と定める.ただし, rad は「ラジアン (radian)」と読む. 正確には,「円弧と半径が等しいときの中心角一、弧度與扇形周長與面積 (1)弧度制: (a)弧度量的定義: 設有一圓,圓心為O,半徑為r。在圓周上取一段圓弧 ∩ PQ ,使得圓弧 ∩ PQ 的 長度等於r,規定這一段圓弧 ∩ PQ 所對的圓心角∠POQ就定義成1 弧度。 (b)度與弧度之互換:
功課幫
扇形面積 公式 弧度法
扇形面積 公式 弧度法- 弧度法の便利な点 扇形の弧の長さと面積の公式は流れを押さえるべし 扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援扇形的弧長與面積公式: 若圓半徑為 r,扇形 COD 的圓心角 ∠COD=θ(弧度),2π, ≤ θ 0 ≤ 如下圖所示,令扇形的弧長為 s,面積為 A,則:




1 1 2 弧度制和弧度制与角度制的换算学案 含答案 七七文库www 77wenku Com
弧度 b 1弧度=180 ° π c 扇形弧長S=rθ d 扇形面積A=1 2 r2θ=1 2 rS (2)三角函數的定義 正弦函數sinA=∠ 的對邊 斜邊 餘弦函數cosA=∠ 的鄰邊 斜邊 正切函數tanA=∠ 的對邊 ∠ 的鄰邊 餘切函數cotA=∠ 的鄰邊 ∠ 的對邊 正割函數secA= 斜邊 ∠ 的鄰邊 餘割函數cscA= 斜邊 ∠ 的對邊 (弧度制)循环链条扇形面积计算公式: 扇形面积S=圆心弧度绝对值a×半径r² / 2 圆心弧度绝对值a =扇形面积S×2 /半径r² 弧长L=圆心弧度绝对值a×半径r 扇形面积S=弧长L×半径r / 2 弧长公式: l = n(圆心角)× π(圆周率)× r(半径)/180=α(圆心角弧度数)× r(半径) まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の
扇形の弧の長さと面積の公式 弧の長さと面積の公式 半径 \(r\),中心角 \(\theta\mathrm{rad}\) の原形の弧の長さを\(l\),面積を\(S\)とすると ・弧の長さ\(l\) \(l=r \theta\)翻轉學習影片描述:講師政治大學 施政丞 講師簡介 目前就讀於國立政治大學應用數學所。 喜愛運動與大自然,個性熱情奔放,對於教學有極大的熱忱。數學對我來說就是趣味的來源,希望透過這個計畫讓同學們對數學產生熱情。 影片簡介 介紹如何將度度量轉換為徑度量並運用在弧度量:弧度量的定義,弧長與扇形面積,計算機的rad鍵 三角的和差角公式:正弦與餘弦的和差角、倍角與半角公式 三角函數的圖形:sin, cos, tan 函數的圖形、定義域、值域、週期 性,週期現象的數學模型。 正餘弦的疊合:同頻波疊 合後的頻率、振幅。 三角函數
(4)陰影部分面積=四邊形oapb面積-扇形oab面積 練習 11 如圖,圓 o的半徑是10公分,有一圓心角 ,則: (1)此圓心角所對弧的長度是多少公分? (2)圓心角 所圍扇形的面積是多少平方公分? 練習 12 如圖, o為圓心,a、b為圓o上兩點。S63 圓周率、圓周長、圓面積、扇形面積:用分割說明圓面積公式。求扇形弧長與面積。知道以下三個比相等:(1)圓心角:360;(2)扇形弧長:圓周長;(3)扇形面積:圓面積,但應用問題只處理用(1)求弧長或面積。 學習表現: sⅢ2 認識圓周率的意義中1数学 中学数学3分で簡単にわかる!「扇形(おうぎ形)の面積の求め方」の公式 中1数学 中学数学速さの単位変換・換算の2つの方法弧度を使って弧の長さと面積を求める このテキストでは、弧度を使って弧の長さと面積を求める方法を解説しています。 半径がrで中心角がθの扇の弧の長さをl




50 扇形面積公式弧長 最高のぬりえ



扇形弧长公式 搜狗图片搜索
扇形面积公式 扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。 数学公式表示为:S扇=(lR)/2 (l为扇形弧长) = (1/2)θR² (θ为以弧度表示的圆心角)。關 鍵 字: 三角函數、函數與方程式及其圖形、弧度、弧長、扇形面積公式 授權資訊: 創用cc 姓名標示非商業性相同方式分享 25 台灣 作者: 旭聯科技 (數位典藏與數位學習國家型科技計畫第六分項子二計畫) 作者: 陳燕靜 (市立成功國小) 提供者:扇形の面積・弧の長さ・まわりの長さの求め方公式 =直径×円周率× 中 心 角 360 ° +半径×2 ピタグラスの定理(三平方の定理)により,横の長さが Δx,縦の長さが Δy である直角三角形の斜辺の長さ ΔL は したがって x ,y 直交座標では x=t とおけば上記の公式が得られる.



扇形面积公式扇形面积计算公式 天奇生活




1 1 2 弧度制和弧度制与角度制的换算学案 含答案 七七文库www 77wenku Com
弧度法の定義は扇形の弧の長さ を半径 で割ると, 角 が求まるというもので, 以下の式で定義されます。 この定義から, 扇形の弧の長さ は, と導け, 扇形の面積 は, 度数法の公式 をradに置き換えて, また, 扇形の弧の長さの公式より, なので, となり, 以上より おうぎ形の面積を求める公式 面積=円の面積×中心角の割合 半径5cm、中心角36度のおうぎ形の面積は何cm 2 計算方法は加減法または代入法で選択でき、途中式も表示されます。 弧度法 (ラジアン)今までの角度 (0°,180°,360°等)=度数法 (「°」 図解講師「爽茶」の最高に分かりやすいサイト そうちゃ's 図解英数ゼミナールしかし,円周の長さ,円の面積など長さや面積を數A 數B 11常用的三角比公式 • 和角公式與差角公式 • 二倍角公式 • 半角公式 X 12弧度量 弧長與扇形面積 11 弧度量 弧長與扇形面積 13三角函數的圖形 正弦(sin) 函數的圖形



高一 三角函数 任意角的概念 弧度制 扇形面积公式练习题 19 11 5




2 圓心角所對弦長 弧長與扇形面積 基本觀念 國三上2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube
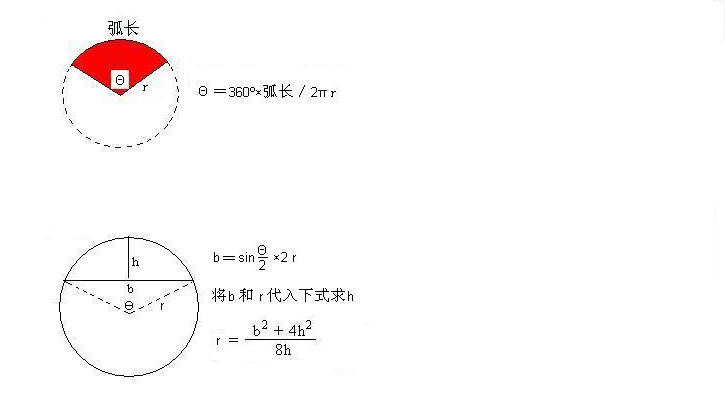
計算弓形面積 張貼者: 10年11月2日 下午719 pegasus@ymshtpedutw 已更新 10年11月2日 下午902 弓形面積公式: 註 :當張角超過 180° 時,此公式仍然是正確的。 參考網頁: 維基百科 Circular Segment (弓形) 註:弓形的張角單位為「弧度」。 1 つ目の式を 2 つ目に代入するだけです。 1 つ目の式から θ = l r とできますので、弧度法の角度 θ を消せば S = 1 2 r 2 θ = 1 2 r 2 × l r = 1 2 r l となります。 もし 半径と弧の長さがわかっているのであれば 、その情報だけで 扇形の面積が出せる公式 です 弧度法における面積公式 半径 r r r ,中心角 θ \theta θ ラジアンの扇型の面積は 1 2 r 2 θ \dfrac{1}{2}r^2\theta 2 1 r 2 θ 例えば,半径が 2 2 2 で中心角が π 4 \dfrac{\pi}{4} 4 π ラジアンである扇形の面積は, 1 2 × 2 2 × π 4 = π 2 \dfrac{1}{2}\times 2^2\times\dfrac{\pi}{4}=\dfrac{\pi}{2} 2 1 × 2 2 × 4 π = 2 π と計算できます。



Q Tbn And9gcqfw55qjcehhr0gshvtjmvndimg 6cichotlqsmxagwttsukyzu Usqp Cau




2 3 弧度制一 素质教育目标 一 知识教学点1 弧度制的定义 2 用弧度制表示的弧长公式 扇形面积公式 Ppt Download
(弧度制)循环链条扇形面积计算公式: 扇形面积S=圆心弧度绝对值a×半径r² / 2 圆心弧度绝对值a =扇形面积S×2 /半径r²扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。 扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア 扇形の弧の長さの求め方 公式と計算例 弧度法の便利な点 扇形の弧の長さと面積の公式は流れを押さえるべし 弧度法の便利な点 扇形の弧の長さと面積の公式は流れを押さえるべし



弧长公式 扇形面积公式 圆 中考网



细品教材 一 弧度制 1 1弧度的角 把长度等于半径长的圆弧所对的圆心角叫做1弧度的角 用符号rad表示 读作弧度 如图1 1 2 1 1 劣弧 R 所对的圆心角 Aob就是1弧度的角 记作 Aob 1 Rad 如图1 1 2 1 2 劣弧 1 5r 所对的圆心角 Aoc就是1 5
円弧の長さ xsrvjp おうぎ形の弧の長さ = 直径 × 314 × 中心角 ÷ 360 円の面積 = 半径 × 半径 × 円周率 弧の面積 = 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 名前に「弧」とついているように,円の弧を使って定義します. 弧度法 半径1の扇形の弧の長さが弧度法で扇の弧の長さと面積を求める公式 弧度法を使って、扇の弧の長さと面積を求める公式を紹介します。 半径がr、中心角がθの扇の弧の長さをl、面積をSとするとき ※θは、度数法ではなく弧度法弧度公式(弧度計算公式)由滬江高考資源網提供,小學數學幾何形體周長 面積 體積計算公式 長方形的周長=(長寬)×2 C=(ab)×2 正方形的周長=邊長×4 C=4a 長方形的面積=長×寬 S=ab 正方形的面積=邊長×邊長 S=aa= a 三角形的面積=底×高÷2 S=ah÷2 平行四邊形的面積



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




高中数学思维导图 高中数学必修4第一章三角函数的思维导图 Math实验室
まず、お馴染みの扇形の面積の公式を書いて、角度のところのみ弧度法で書きます。 さらに前述の 弧の長さの公式 を当てはめると、 (半径)×(弧の長さ)÷2 というかなりシンプルな式になります。例1(1) (2)各為多少度? Ans: 例2是多少弧度? Ans: 例3有一扇形的周長度量與面積度量相同,若圓心角為,求圓半徑r (以表示) Ans: 例4某時鐘時針長2公吋,分針長3公吋,問 分鐘內時針尖端移動多少公吋? 分鐘內分針掃過的面積為多少? 面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。




弧長計算公式 弧長公式 N是圓心角度數 R是半徑 L是圓心角弧長 L 華人百科




弧度制 教案5下载 Word模板 爱问共享资料
弓形の面積 弓形とは円とその割線 (円と異なる二点で交わる直線)で囲まれる図形で、図1における網掛け部分のような図形です。 実はその反対側も弓形です。 以下では弓形の面積をS、円の半径をr、弓形の基になる扇形の中心角をθとします。 但し、中心 「扇形の弧の長さ」と「扇形の面積」の公式を用いれば中心角を削除することができます。 『\(S=\dfrac{1}{2}lr\)』というように面積を半径と弧の長さから求めることができるのです。 上記の例題の場合、\(S=\dfrac{1}{2}×10{\pi}×6=30\pi\) 答えは\(30{\pi}cm^{2}\)です。 "扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明



扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili




圆扇形与弓形



扇形的周长和面积公式是什么 酷知经验网




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌



功課幫




Ppt 弧度制powerpoint Presentation Free Download Id



扇形面积公式弧度制 弧度制求扇形面积公式 江苏凤巢网络



扇形的体积公式 土嘎嘎




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌



360影视 影视搜索



扇形中心角公式 ニスヌーピー壁紙



扇形面积计算 万图壁纸网




半圆的面积公式怎么求 半圆的面积公式中文 半圆的面积怎么求



Q Tbn And9gcqgejm7nbeljjpoq4j3gwoy4cch2aapovxhwfsr Y2ji7bsp4dn Usqp Cau



弧形的面积公式 西瓜视频搜索



扇形面积公式小学 初三网



弧度制下的扇形问题 1 1任意角的概念与弧度制 高中人教b版 数学中国网



弧度制扇形面积公式高中扇形的弧长和面积公式 图文 叽叽歪歪吧




弓形 圆弧形的面积 弧长 弦长 弦高 半径 夹角在线计算器 三贝计算网 23bei Com



高一 三角函数 任意角的概念 弧度制 扇形面积公式练习题 19 11 5




扇形計算公式 一條弧和經過這條弧兩端的兩條半徑所圍成的圖形叫扇形 半 華人百科



扇形面积的计算公式 扇形面积的计算公式画法




Hdu5858 Hard Problem 码农家园



扇形面积扇形面积 面积公式 爱华网



已知扇形的面积为2 扇形圆心角的弧度数是4 则扇形的周长为 高中一年级 数学试题 弧度制 弧度与角度的互化考点 好技网




扇形面积公式和扇形弧长公式扇形的所有公式



弧度制 扇形弧长公式 面积公式 数学作业 解题作业帮



弧长及扇形的面积公式 弧长及扇形面积计算公式



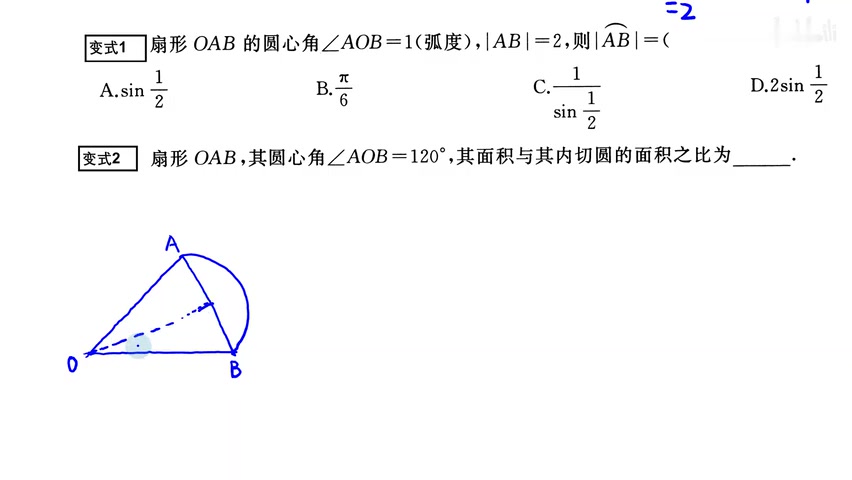
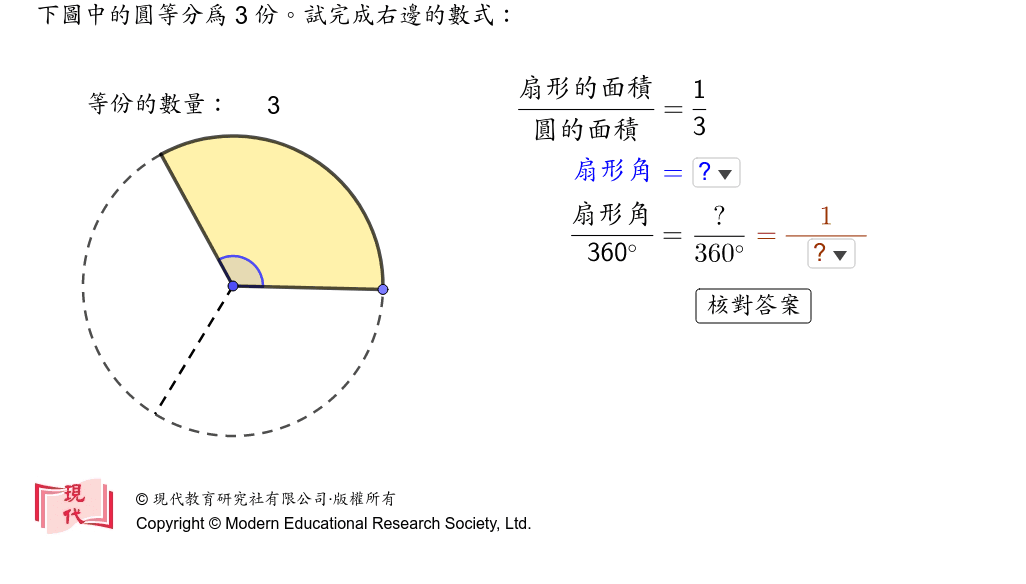
3



17 18版高中数学第一章三角函数3弧度制学案北师大版必修4 Doc 课件巴巴kejian Com 课件巴巴kejian Com




1 1 2 4 扇形面积公式 高中数学必修4 高中数学 辅立码课




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條




扇形有关计算解析 初中数学 新东方在线网络课堂



三角函数度数对照表 信息图文欣赏 信息村 K0w0m Com




扇形弧長 扇形弧長是扇形的兩條半徑之間的圓弧長度 一條圓弧和經過這條圓弧 百科知識中文網




扇形的弧長與面積
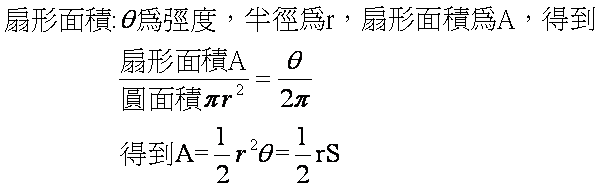



扇形的弧長與面積



弧长及面积公式 腾讯视频



高中数学必修四 基础详细讲义附答案38页 小初高题库试卷课件教案网



高一 三角函数 任意角的概念 弧度制 扇形面积公式练习题 19 11 5



扇形 圆形计算公式 指南 下载 Word模板 爱问共享资料




圆形面积计算公式r为小圆半径圆的周长c 2p




高一数学 下 利用弧度制证明扇形面积公式s 1 2 Lr



弧长及面积公式 腾讯视频




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條




Ppt 弧度制powerpoint Presentation Free Download Id



扇形面積 面積公式 另解 公式推導過程 中文百科全書




001 弧度 弧長及扇形面積原理 Youtube




扇形计算公式 扇形的面积计算公式



三角公式怎么记 请看这儿




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月



圆的弧长 半径 圆心角在线计算器 在线计算 在线计算器 计算器在线计算




扇形的弧長公式 Youtube




扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube




圆扇形与弓形



题型 2弧长与扇形面积公式的计算 哔哩哔哩 つロ干杯 Bilibili



Ch2三角函數 2 1 2 2 我的m讚



3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili



圆的周长与面积 弧长 扇形的面积 玄数



弧度计算公式 弧度计算公式 弧度 计算 公式



弧長計算公式 計算公式 弧長公式 拓展 例子 補充公式 各種公式 扇形面積 公式 中文百科全書



弧长公式及扇形面积公式设扇形的弧长为l 圆心角为a 弧度 半径为r 则l S扇 作业 慧海网




扇形周长公式和面积公式是什么 星火网校




扇形计算公式 扇形的面积计算公式




极坐标下 定积分求面积公式推导 知乎




扇形面積公式 公式 推導過程 注意事項 中文百科全書



功課幫



扇形面积的计算公式 扇形面积的计算公式画法




扇形的面积 弧长 周长 弦长在线计算器 三贝计算网 23bei Com



弧长公式 弧长公式是什么 弦长弧长计算公式 悦地带图网



公式与弧度的v公式弧长地图扇形的角度公式面积高中钦州 高中课题目




圓面積公式弧度單元四 Bedachun



公式与弧度的v公式弧长地图扇形的角度公式面积高中钦州 高中课题目




弧度角扇形面积 三人行教育网 Www 3rxing Org



扇形面积的计算公式 扇形面积的计算公式画法



六年级扇形面积公式 初三网




扇形计算公式 扇形的面积计算公式




数 你好看 任意角三角函数与诱导公式 知乎



1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆面积s的360分之 扇形的面积公式 1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆 面积s的360分之 扇形的面积公式为 S 作业 慧海网



六年级扇形面积和弧长公式 初三网




高中文科数学1 1 2 弧度制教学反思 莲山文库



Q Tbn And9gctoaftep Cp0mxb1byahotggx3ub73wafwbkzah7fg7xmsh2anr Usqp Cau




数 你好看 任意角三角函数与诱导公式 知乎




弧长计算公式 弧長角度



弧长及扇形的面积公式 弧长及扇形面积计算公式



Sjrc8kt8zjo8hm




高中數學必修 一題多解 三角函數 扇形的面積求法 每日頭條



扇形面积公式讲解 北京爱智康



扇形面积的计算公式 扇形面积的计算公式画法




扇形面積 扇形是與圓形有關的一種重要圖形 其面積與圓心角 頂角 圓半徑 百科知識中文網



0 件のコメント:
コメントを投稿