The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetry Graph of the parabola in vertex form The vertex form of parabola equation is y = a(x h)^2 k , where ( h , k ) = vertex and axis of symmetry x = h The parabola is f(x) = y = 2x 2Algebra Quadratic Equations and Functions Quadratic Functions and Their Graphs 1 Answer Nallasivam V Refer explanation section Explanation Given #y=2x^24# To find the vertex, rewrite the function as
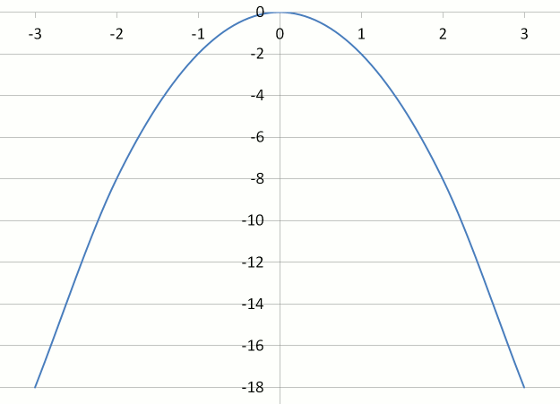
Parabolas Xcelerate Math
Graph the parabola y=2x^2-5x-3
Graph the parabola y=2x^2-5x-3-Also graph the parabola If you can please include the points that I have to graph/plot that would be great I know how to get the vertex but I always mess up when it comes to graphing the exact point or points Answer by ewatrrr() (Show Source)The focus of a parabola can be found by adding to the ycoordinate if the parabola opens up or down Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus
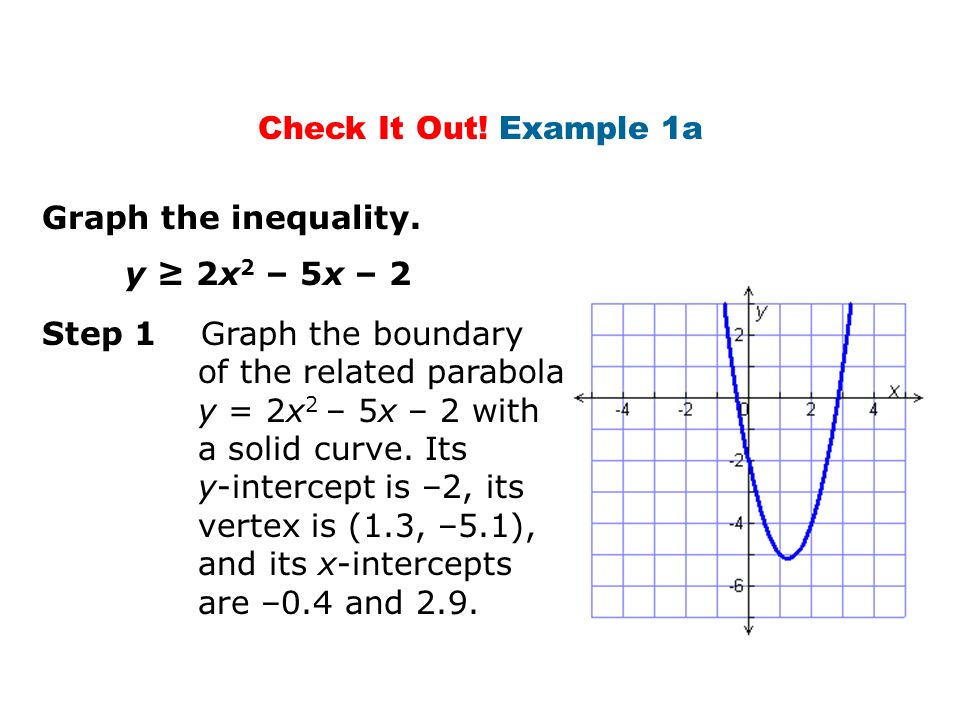



Warm Up 1 Graph The Inequality Y 2x 1 Solve Using Any Method 2 X 2 16x 63 X 2 8x 3 7 Ppt Download
Graph y=2x^216x28 y = 2x2 − 16x 28 y = 2 x 2 16 x 28 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 − 16 x 28 2 x 2 16 x 28 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a aJenna from SVSU Micro Math helps you graph a parabolaProblem Graph the parabola y = 2x^2 2x 3Level intermediate/college algebra#SVSUmicromathLet's graph y=2x 2x (red) and y=2x 24x (blue) The vertex when a =2 and b =1 is at x=¼, and the vertex when a =2 and b =4 is x=1 Now, we see that our hypothesis is not completely correct, for – b /2 for the first graph would give us ½, but we have ¼ Instead, it must be – b /2 a since a =1 on our previous graphs and that works
Algebra > Graphs> SOLUTION Graph the parabola y=2x^24x6 on graph paper Log On Algebra Graphs, graphing equations and inequalities Section Solvers SolversGraph the parabola and give its vertex, axis of symmetry, intercepts, and y intercept y = 3x^2 6x 10 The vertex is (Type an ordered pair) The axis of symmetry is Type an equation Use integers or Select the correct choice below and fill in any answer boxes within your choice The xintercepts are at x (Type an exact answer, using radicalsClick here to see ALL problems on Graphs Question 6355 Graph the parabola y= 3/2 x^2 Answer by MathLover1 () ( Show Source ) You can put this solution on YOUR website!
View interactive graph > Examples (y2)=3(x5)^2;To find the vertex, we first need to find the axis of symmetry (ie the xcoordinate of the vertex) To find the axis of symmetry, use this formula From the equation we can see that a=2 and b=8 Plug in b=8 and a=2 Multiply 2 and 2 to get 4 Reduce So the axis ofQuestion Graph the parabola y=x^210x Plot the vertex and four additional points, two on each side of the vertex Answer by josgarithmetic() (Show Source) You can put this solution on YOUR website!



Solution Sketch The Graph Of The Function Y 2x 2 4x 5



Key To Practice Exam Ii
Graph the parabola y = 2x^2 To graph the parabola, plot the vertex and four additional points, two on each side of the vertex Then click on the graph icon The standard form of parabola equation is y = a(x h)^2 k, where (h, k) = vertex and axis of symmetry x = h The parabola is y = x 2 6x Wrote the equation in standard form of a parabola eqaution To change the expression x 2 6x into a perfect square trinomial add and subtract (half the x coefficient)² Here x coefficient = 6 so, (half the x coefficient)² = (6/2) 2 = 9Below is an animation of the lines tangent to y=x^2 at each point



Quadratics In Context Nz Maths
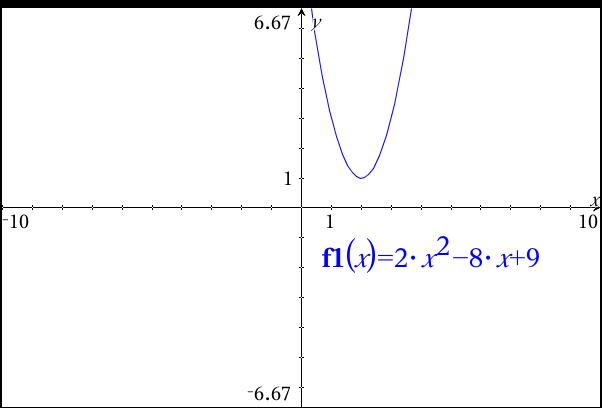



What Is The Graph Of The Parabola Represented By Y 2x 2 8x 9 Socratic
Identify at least the xcoordinate of the vertex How do you graph the parabola #y= 2x^24# using vertex, intercepts and additional points?The graph of a quadratic equation in two variables (y = ax 2 bx c) is called a parabolaThe following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot



Solution Graph The Quadratic Equation Y 2x 2 What Is The Vertex Also Graph The Parabola If You Can Please Include The Points That I Have To Graph Plot That Would Be G
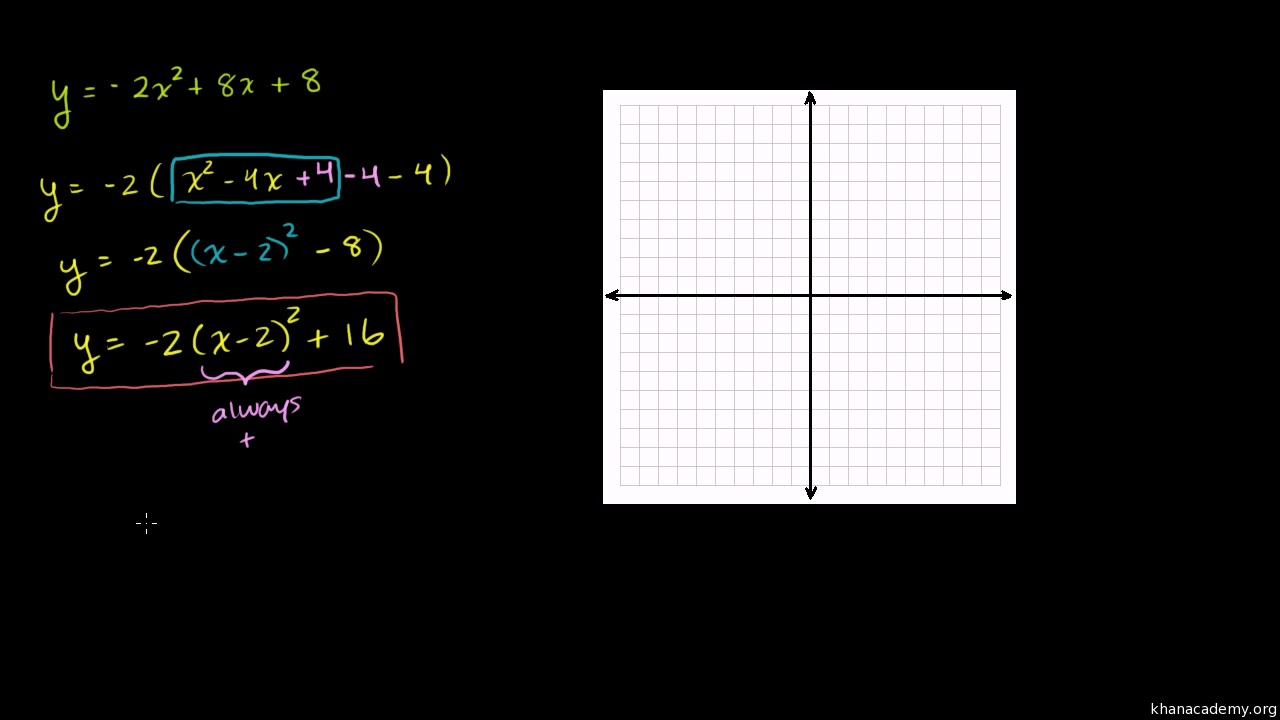



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy
Released under CC BYNCSA http//creativecommonsorg/licenses/byncsa/30/legalcodeGraphing a basic parabola using y=3x^2 to show the use of a table and keGraph y^2=x y2 = x y 2 = x Rewrite the equation as x = y2 x = y 2 x = y2 x = y 2 Divide each term by and simplify Tap for more steps Divide each term in x = y 2 x = y 2 by x = y 2 x = y 2 Cancel the common factor ofGraph the parabola and give its vertex, axis, xintercepts, and yintercept y = 2x^2 32x 126 The vertex is x= 0 x = 2 x = 7 x = 8 Select the correct below and fill in any answer boxes within your choice The xintercepts are at x = There is no xintercept The yintercept is at y = Chose the correct graph of the function y = 2x^2 32x 126 below



Solution Graph Y 2x 2 4x



Quadratics Graphing Parabolas Sparknotes
The equation of parabola can be expressed in two different ways, such as the standard form and the vertex form The standard form of parabola equation is expressed as follows f (x) = y= ax2 bx c The orientation of the parabola graph is determined using the "a" value If the value of a is greater than 0 (a>0), then the parabola graphIn the figure, the vertex of the graph of y=x 2 is (0,0) and the line of symmetry is x = 0 Definition Parabola 1Algebric A Parabola is the graph of a quadratic relation of either form where a ≠ 0;Question 6525 Graph the quadratic equation y=2x^2 What is the vertex?



What S The Axis Of Symetry Vertex And Graph Y 2x 2 6x 1 Mathskey Com




Please Help Thank You The Graph Of The Function Y X2 Is Shown How Will The Graph Change If Brainly Com
Refer to the explanation Graph y=2(x1)^23 This is a quadratic equation in vertex form y=a(xh)^2k, where a=2, h=1, k=3 The vertex is the point (h,k), which is (1,3) Plot this point The yintercept is the value of y when x=0 Substitute 0 for x and solve for y y=2(01)^23 y=2(1)^23 y=2(1)3 y=23 y=1 The yintercept is (0,1) Plot this point To find the xExploration of Parabolas By Thuy Nguyen In this exploration we want to see what happens when we construct the graphs for the parabola y = ax 2 bx c with different values of a, b, and c We'll start first by constructing the graphs for y = ax 2 with different values of a The following are graphs for a = 2, 1, 2, in blue, purple, and red respectivelyIn the theory of quadratic forms, the parabola is the graph of the quadratic form x 2 (or other scalings), while the elliptic paraboloid is the graph of the positivedefinite quadratic form x 2 y 2 (or scalings), and the hyperbolic paraboloid is the graph of the indefinite quadratic form x 2 − y 2 Generalizations to more variables yield
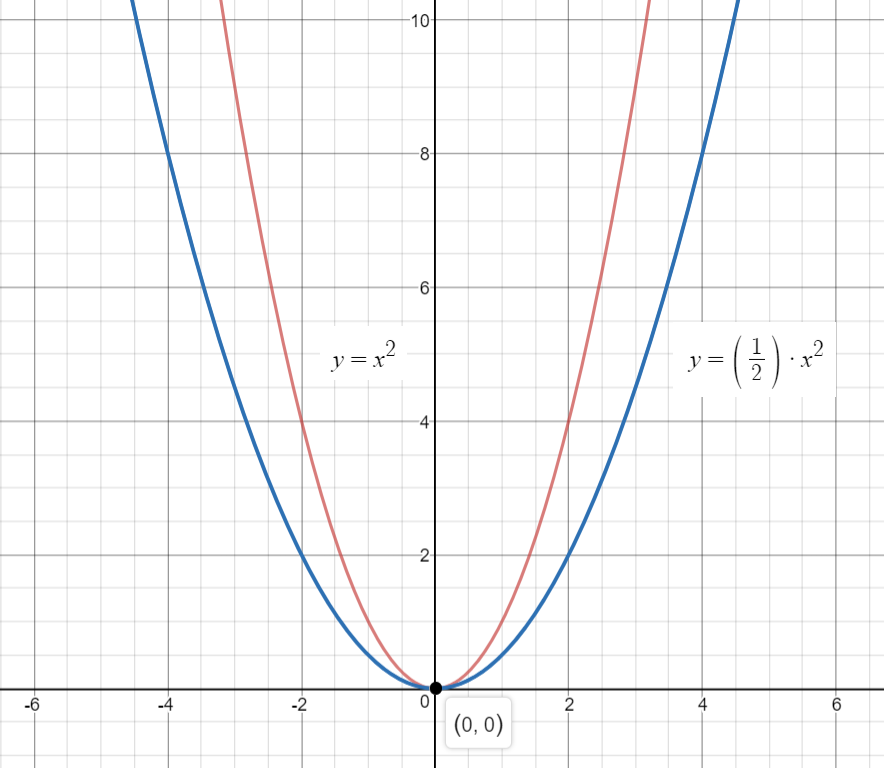



How Do You Sketch The Graph Of Y 1 2x 2 And Describe The Transformation Socratic



How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic
Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Graph Hide Plot »The "formula" for a parabola (in the conic sections form) is mathx^2=4cy/math (although some textbooks use mathp/math instead of mathc/math, so mathx^2=4py/math) If you put your equation into that form you can make some observatioA parabola is the graph of a quadratic polynomial in one variable (see more in the Polynomials section) Its general equation comes in three forms \begin{array}{l l} \text{Standard form } & y = ax^2 bx c \\ \text{Vertex form } & y = a(xh)^2 k \\ \text{Factored form } & y = a(xr)(xs) \end{array} The factored form of the equation
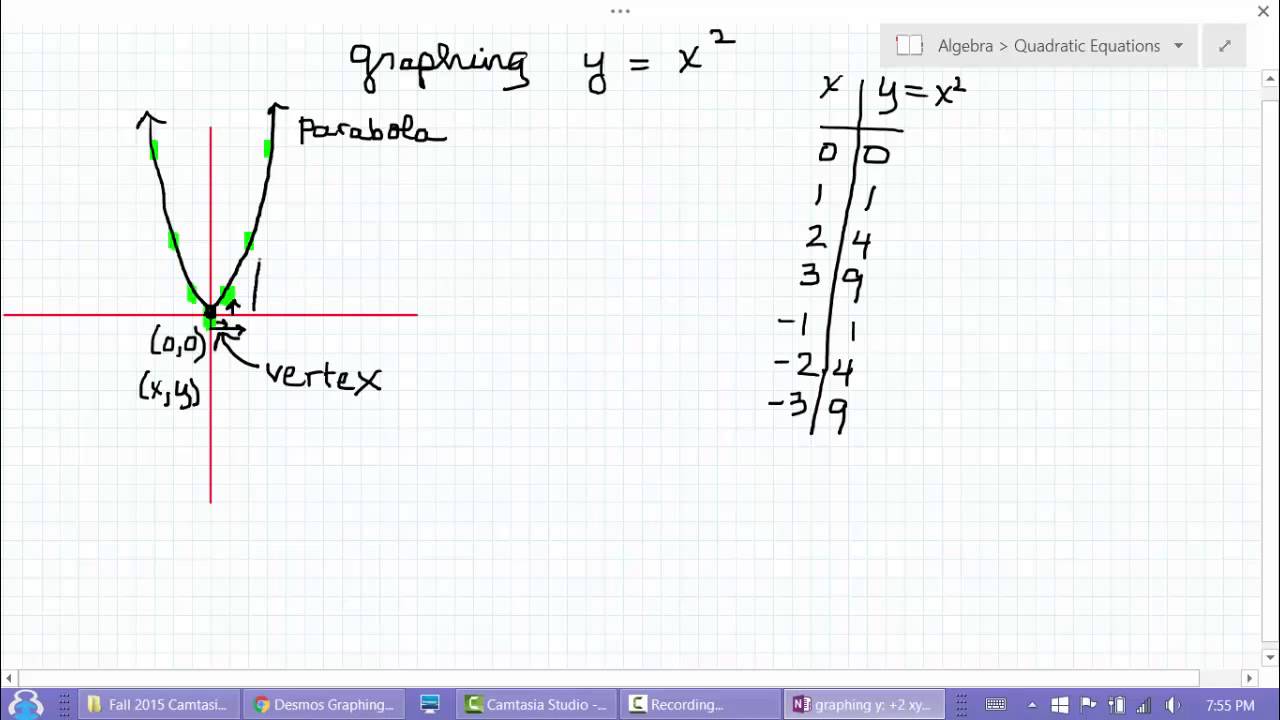



Graphing Basic Parabola Y X 2 Youtube




Use The Parabola Tool To Graph The Quadratic Function Y 2x2 12x 14 Graph The Parabola By First Brainly Com
Graph the parabola {eq}y = 2x^2 12x 16 {/eq} Parabola A parabola is a Ushaped graph, which may open in any direction The direction of opening is described by the value of "a" in theGraph the parabola {eq}y=2x^28x4 {/eq} Construct the graph that illustrates the parabola {eq}y=2x^212x15 {/eq} Determine which graph illustrates theGraph y=2x^212x10 y = −2x2 12x − 10 y = 2 x 2 12 x 10 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for − 2 x 2 12 x − 10 2 x 2 12 x 10 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the



Stephani Eckelkamp The Parabola Friend Of Foe The Graph Of A Parabola Y X2 Has A Vertex At 0 0 The Graph Is Shown Below Now Let Us Look At The Graph Y Ax2 Where A 1 2 3 10 1 3 And 1 10 And When A 1 2 3 10 1 2 1 3 And 1 10




This Graph Represents The Equation Y 2x2 Function Png Image Transparent Png Free Download On Seekpng
Every parabola has an axis of symmetry which is the line that divides the graph into two perfect halves On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equationFirst, graph \(y=2x^2\) Since, the inequality sing is \(>\), we need to use dash lines Now, choose a testing point inside the parabola Let's choose \((0,2)\) \(y>2x^2→2>2(0)^2→2>0\) This is true So, inside the parabola is the solution section Exercises for Graphing Quadratic inequalities Sketch the graph of each function \(\colorAnswer choices The axis of symmetry is x = 1 The vertex is (1,3) The "a" coefficient is positive The parabola has two positive xintercepts y = 2x 2 y = 1/11x 2 y = 1/5x 2 s Question 21 SURVEY



Quadratic Graph Example Y Ax C Expii



How Do You Graph Y 2x 2 4x 3 Mathskey Com
When graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aGraph y=2x^216x30 y = −2x2 16x − 30 y = 2 x 2 16 x 30 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for − 2 x 2 16 x − 30 2 x 2 16 x 30 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find theBelow is the graph of y = x^2 and the line tangent to it at the point (1,1) Use the graph to calculate the rate of change of y =x^2 at the point (1,1) Do you think the rate of change will be the same at every point on the parabola?
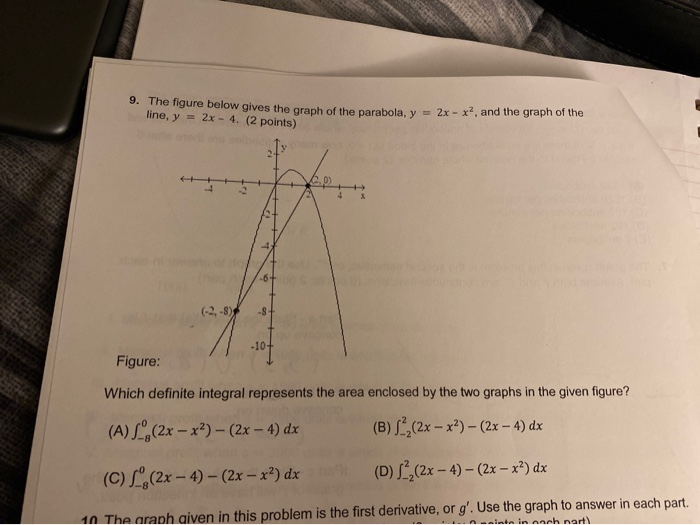



9 The Figure Below Gives The Graph Of The Parabola Chegg Com




Solution Find The Equation Of The Axis Of Symmetry Of The Function Y 2x 2
Which of the following statements is NOT true for the parabola seen in the graph?Take several values for and find , make a table xy 00 13/2Y = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is




Draw The Graph Of Y 2x 2 And Hence Solve 2x 2 X 6 0




Please Help Asap Correct Answer Only Please The Graph Of The Function Y X2 Is Shown How Brainly Com
Short demo on graphing a parabola by finding the vertex and yintercept, and using the axis of symmetryWell lets find out Remember the vertex form of a parabola is y = a ( x − h) 2 k y=a (xh)^2k y = a ( x − h) 2 k, where ( h, k) (h,k) ( h, k) is the vertex We know that a = − 1 / 2 a=1/2 a = − 1 / 2 and we can read the vertex from the graph The vertex is ( 3, 4) (3,4) ( 3, 4) So we know h = 3 h=3 h = 3 and k = 4 k=4 k = 4
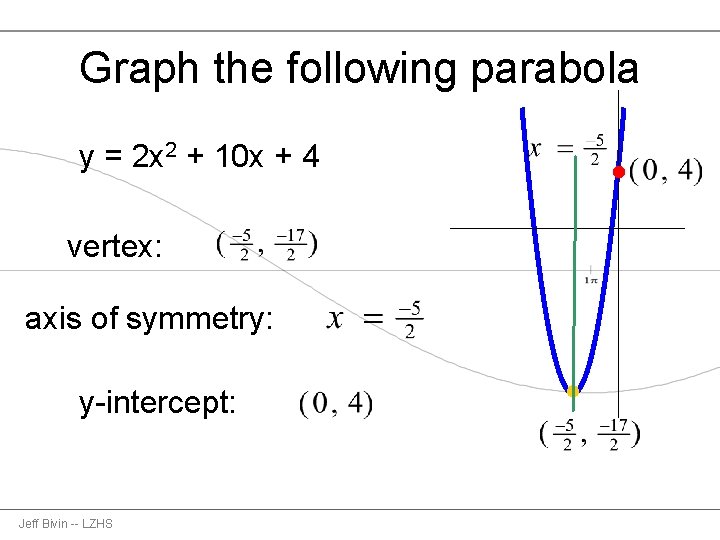



Graphing Parabolas Using The Vertex Axis Of Symmetry



Quadratics Graphing Parabolas Sparknotes
Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three partsParabolas by Becky Mohl Graph the parabola y = 2x^2 3x 4 Now lets change all of the x's in the equation to (x4) and see what happens to the graph As we see in the graph above, the vertex moved over into the 4th quadrant from the 3rd quadrant Why did it do this?Answer to Graph the parabola and give its vertex, axis, xintercepts, and yintercept y=2x^{2}x48 By signing up, you'll get thousands of



Solution Solve And Graph Y 2x 2 8x



Y 2x 2 Youtube
Hi Mike, y = x 2 2 is a quadratic equation of the form y = ax 2 bx c, let a = 1, b = 0 and c = 2 You can certainly plot the graph by using values of x from 2 to 2 but I want to show you another way I expect that you know the graph of y = x 2 If you compare the functions y = x 2 and y = x 2 2, call them (1) and (2), the difference is that in (2) for each value of x the{eq}y=2x^28x16 {/eq} The Parabola It can be noted and notices that the quadratic equations are generally the equation of the parabola, either upward or downward facedAxis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=2x^{2} en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice and dedication If you want




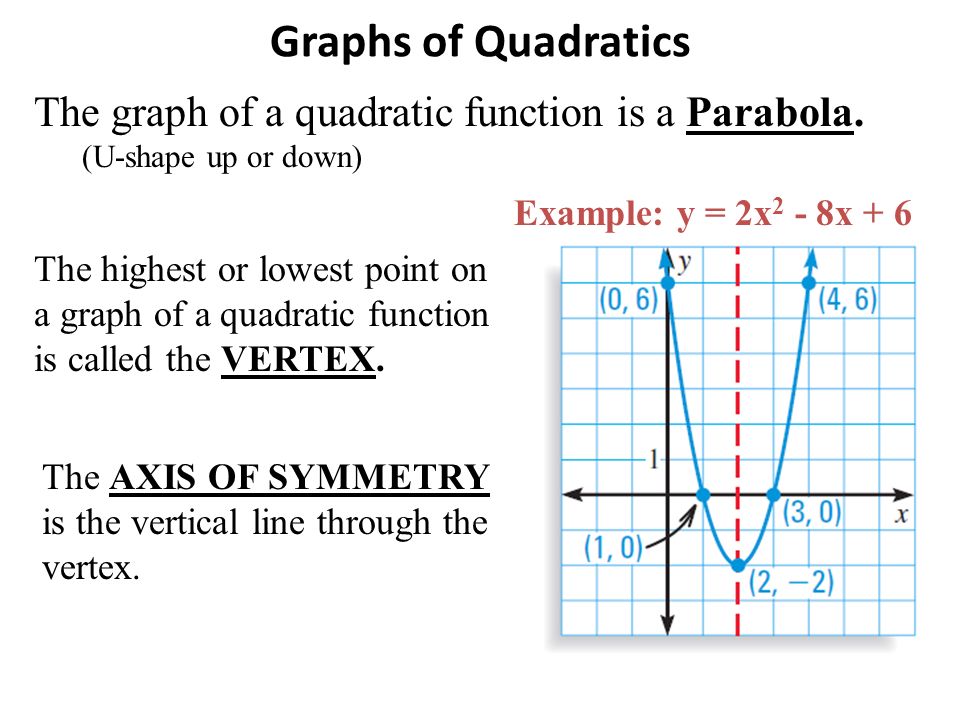
Quadratic Function



Quadratics Graphing Parabolas Sparknotes
Answer to Graph the parabola and give its vertex, axis, xintercepts, and yintercept y = 2x^2 24x 54 By signing up, you'll get thousands ofGraph a parabola by finding the vertex and using the line of symmetry and the yinterceptKey Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;



Exploration Of Parabolas




What Is The Area Enclosed By The Parabola Y2 2x And The Line Y 2x Quora
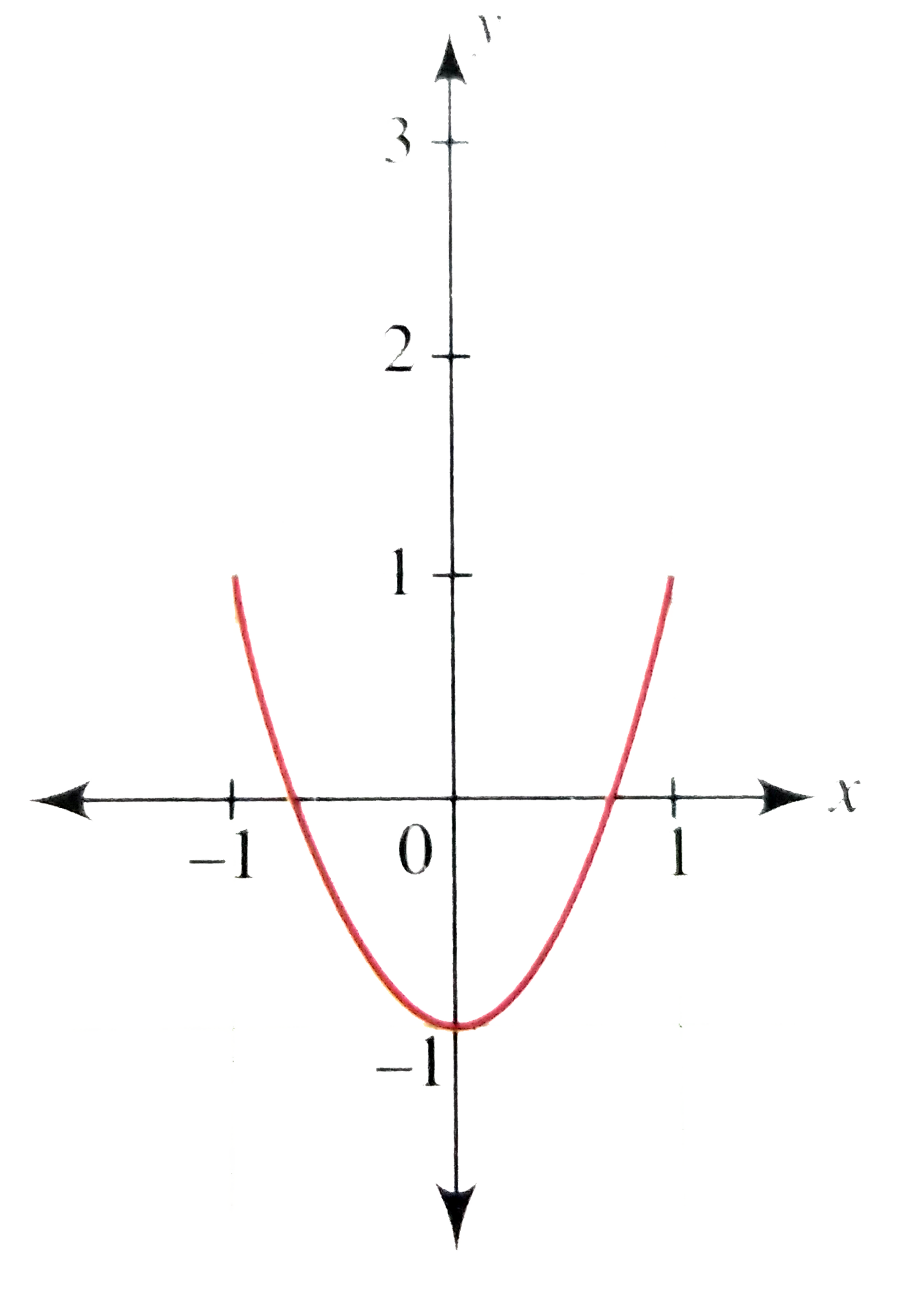



Draw The Graph Of Y 2x 2 1 And Heance The Graph Of F X Cos



Quadratics




Parabola Sketching Y 2x 2 4x 6 From The Parabola Translation Download Scientific Diagram




Classzone Chapter 4



Quadratics Graphing Parabolas Sparknotes



1



Instructional Unit The Parabola Day 4 And 5




How To Draw Y 2 X 2




Graph The Parabola And Give Its Vertex Axis X Intercepts And Y Intercept Y 2x 2 8x 16 Study Com
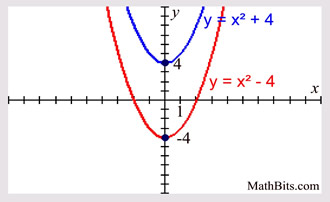



Parabola Parent Function Mathbitsnotebook Ccss Math



Organize The Information For Your Parabola Graph Your Parabola Y 2x 2 12x 19 Axis Of Symmetry Snapsolve



Solution Sketch The Graph Of F X 2x 2 8x 11 It Is A Parabola With Its Lowest Vertex In Which Quadrant Use Window Of 10 To 10 Both X And Y




Graphing Parabolas



Graph Y 2x 2 3x 5 Math Homework Answers



Draw The Graph Of Y 2x 2 X 6 Mathskey Com
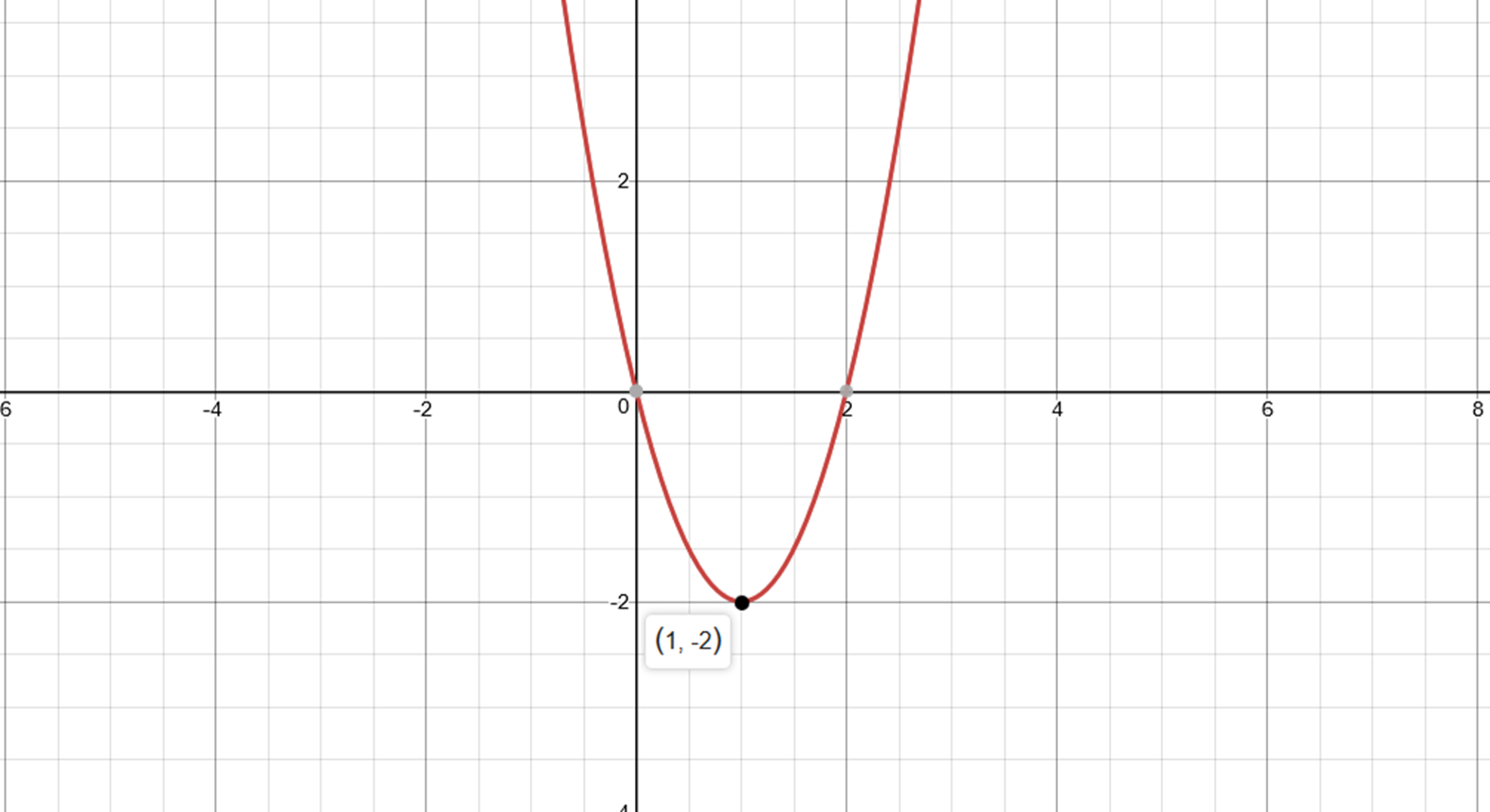



How Do You Find The Vertex Of Y 2x 2 4x Socratic



How To Graph The Parabola Y X 2 6x 11 Quora




Parabolas Xcelerate Math



Mathscene Functions 1 Lesson 3
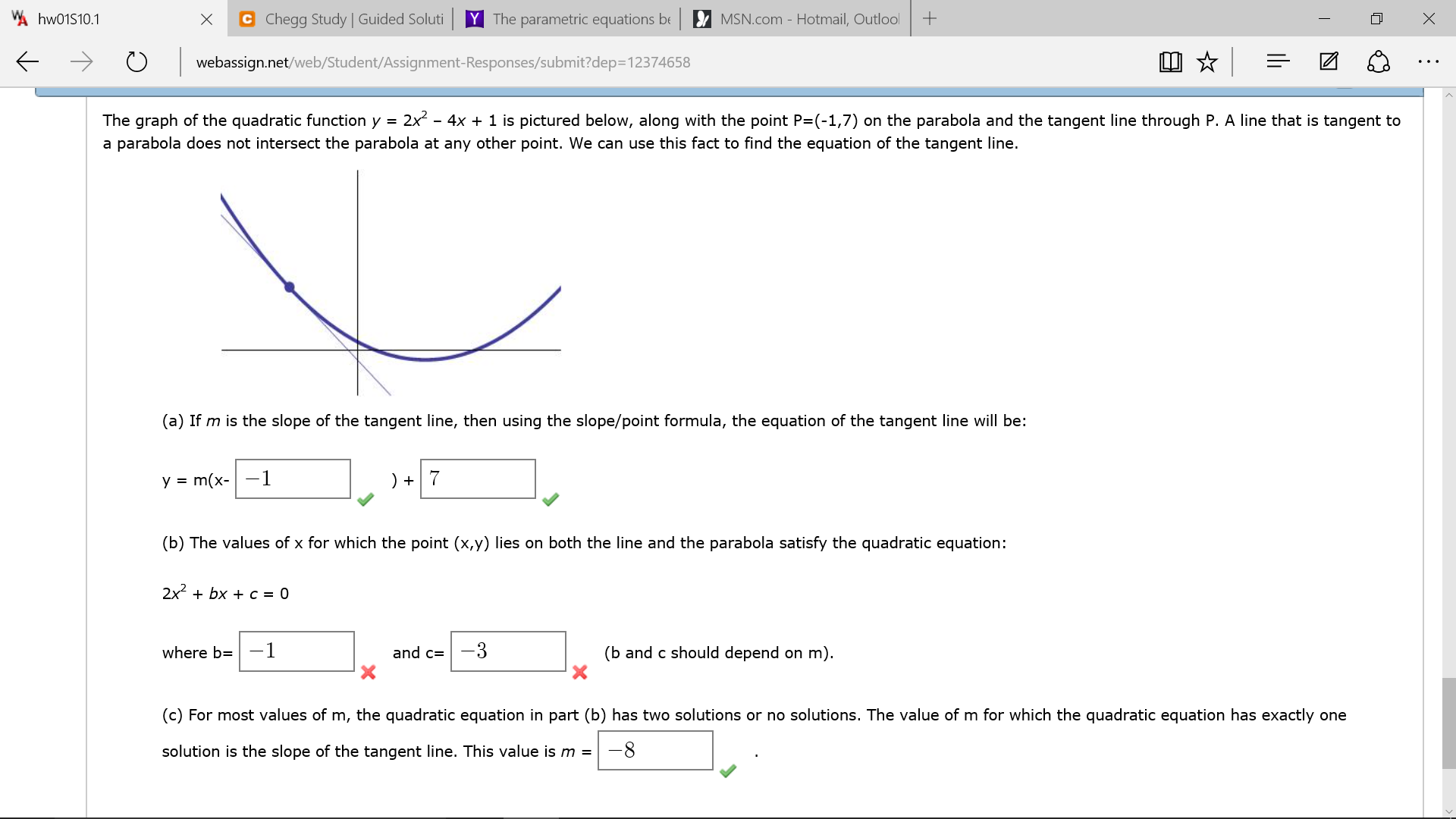



The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com



1
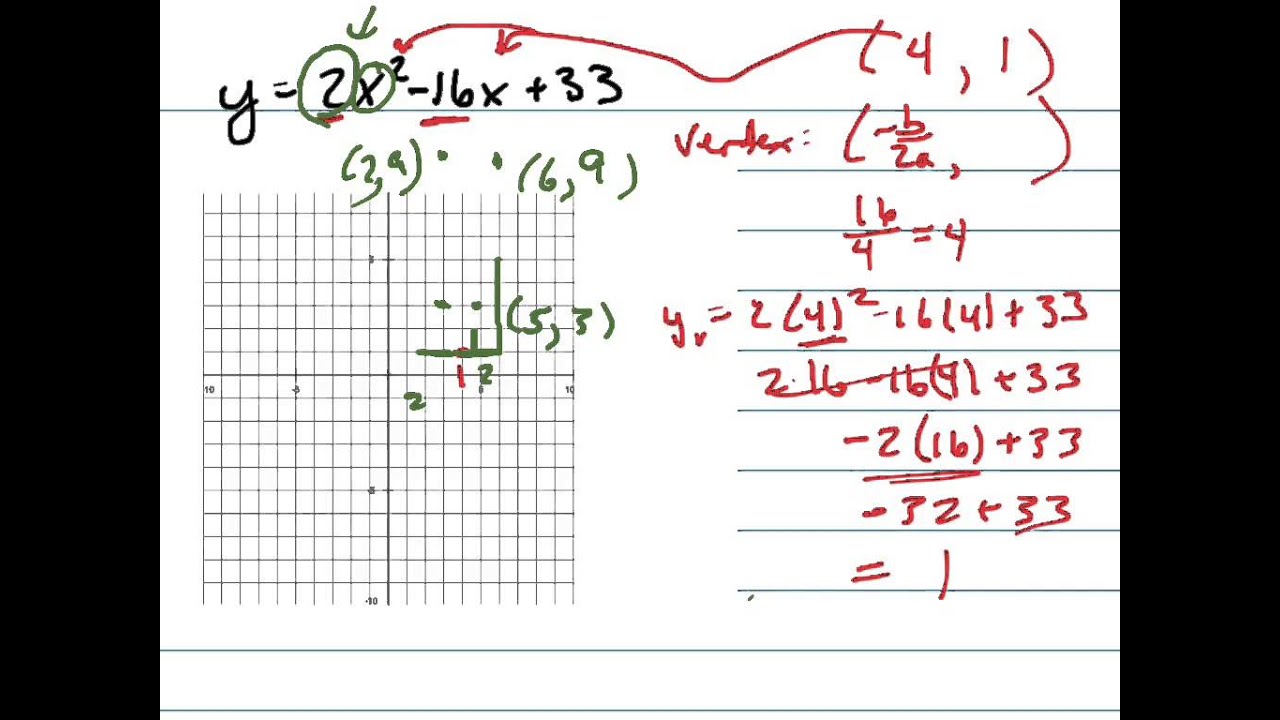



Graph Y 2x 2 16x 33 Youtube




How To Draw Y 2 X 2



What Is The Vertex Of Y 2x 2 4x 12 Socratic




Mfg Graphing Parabolas



What Is The Maxima And Minima Global And Local Of The Function Y 2x X 2 Explain It With The Help Of A Graph Quora



Graphing And Properties Of Parabolas Kuta Software




How To Graph A Parabola 13 Steps With Pictures Wikihow
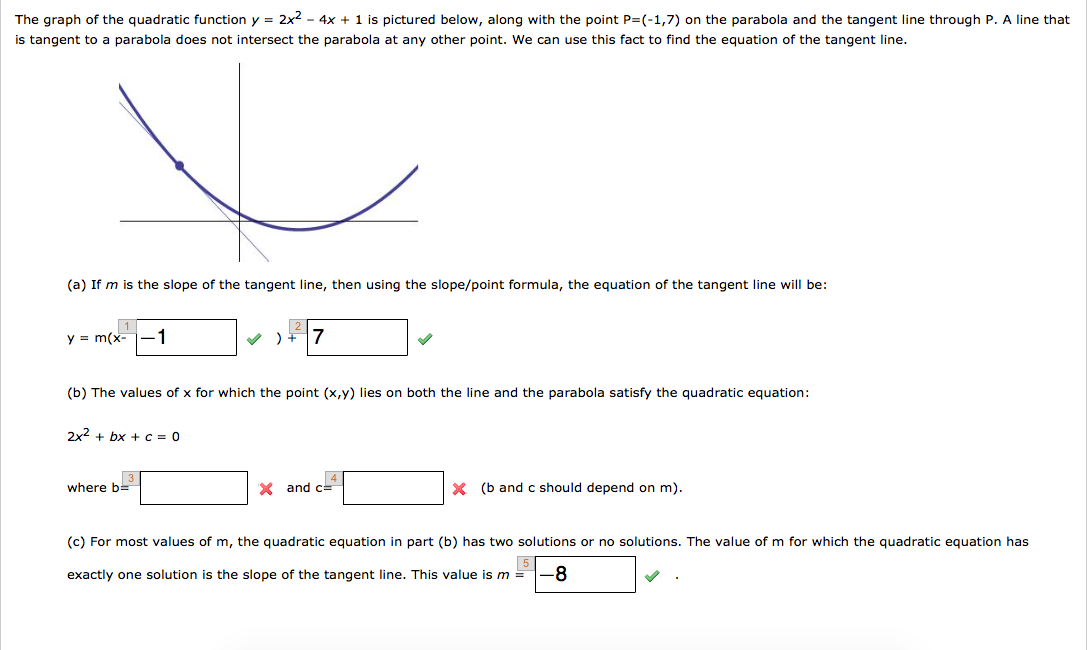



The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com



Parabolas Xcelerate Math




Characteristics Of Parabolas College Algebra



How Do You Graph The Parabola Y 2x 2 9 Socratic




Graphing Parabolas



Solve And Graph Quadratic Function 2x 2 12x 11 Mathskey Com




Warm Up 1 Graph The Inequality Y 2x 1 Solve Using Any Method 2 X 2 16x 63 X 2 8x 3 7 Ppt Download



Maths First Institute Of Fundamental Sciences Massey University
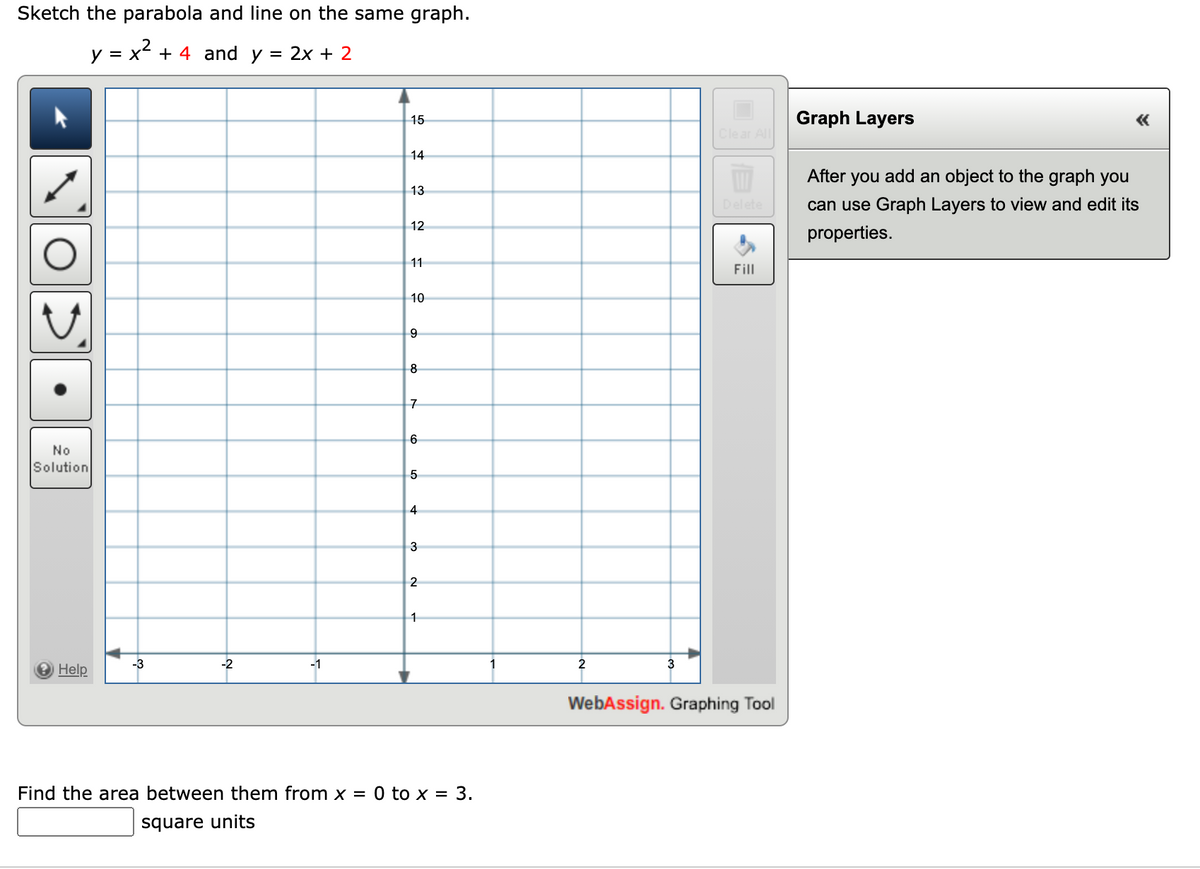



Answered Sketch The Parabola And Line On The Bartleby
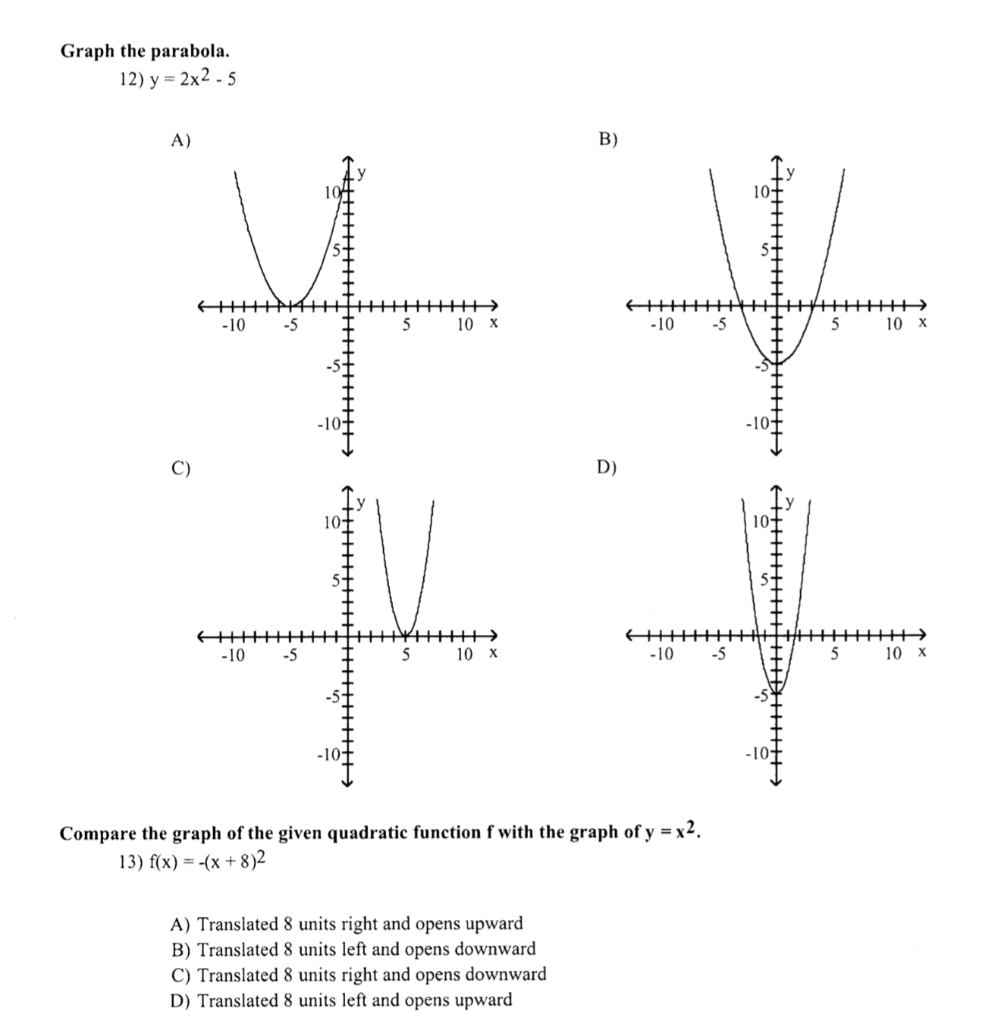



Graph The Parabola 12 Y 2x2 5 A B 10 Chegg Com
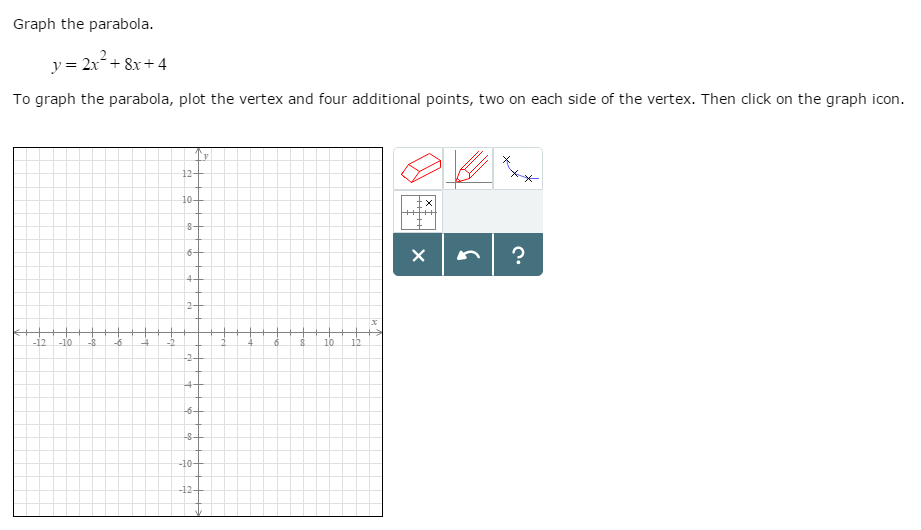



Graph The Parabola Y 2x 2 8x 4 To Graph The Chegg Com



Exploration Of Parabolas
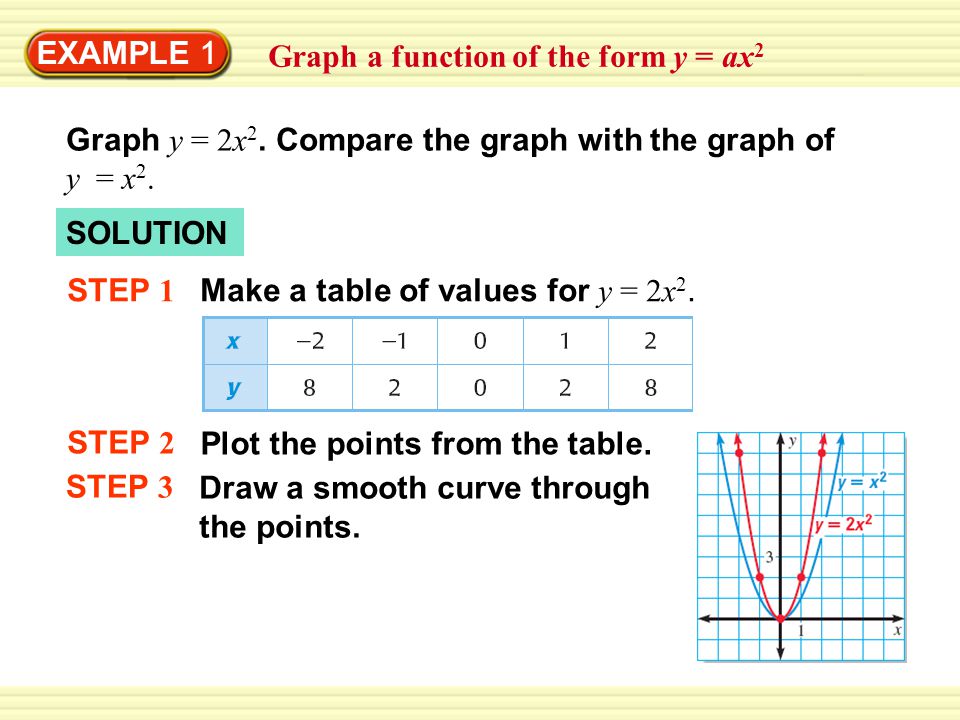



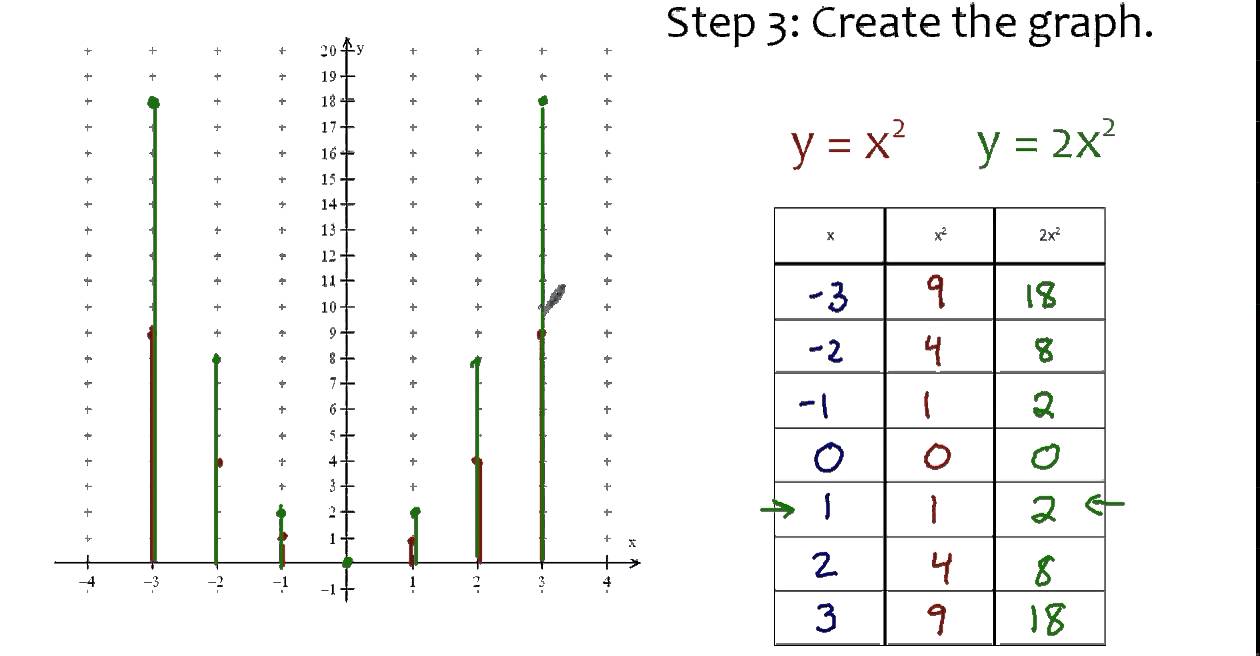
Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download




How To Graph A Parabola 13 Steps With Pictures Wikihow



Warm Up Graphing Using A Table X Y 3x 2 Y 2 Y 3 2 2 8 Y 3 1 Y 3 0 Y 3 1 Y 3 2 2 4 Graph Y 3x Ppt Download



Www K12northstar Org Cms Lib Ak Centricity Domain 4806 Alg1 quadratics packet blank Pdf




Find The Volume Of The Solid Generated By Revolving The Region Bounded By The Graph Of Y 2x 2 1 And Y 2x 12 About The X Axis Round To




Graph The Quadratic Functions Y 2x 2 And Y 2x 2 4 On A Separate Piece Of Paper Using Those Graphs Compare And Contrast The Shape And Position Of The Graphs Study Com
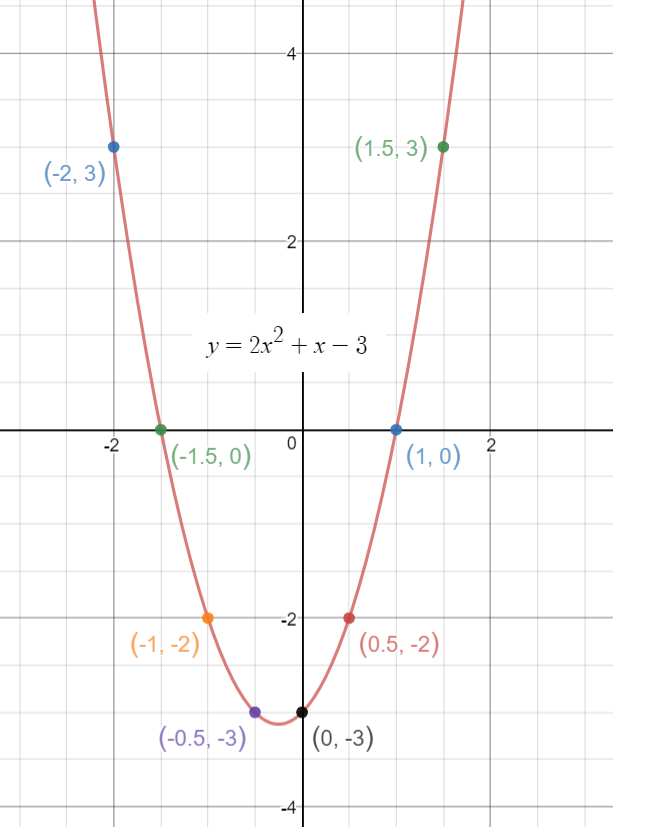



How To Do You Graph Y 2x 2 X 3 By Plotting Points Socratic



Graphing Quadratic Functions
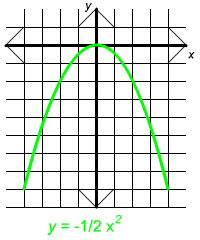



Parabolas And Cubics
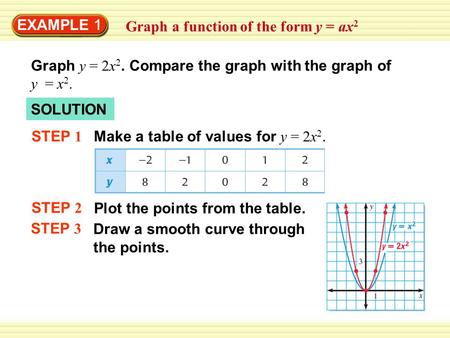



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download



Parabolas



Instructional Unit The Parabola Day 4 And 5




Graphing Quadratic Functions Lesson Article Khan Academy



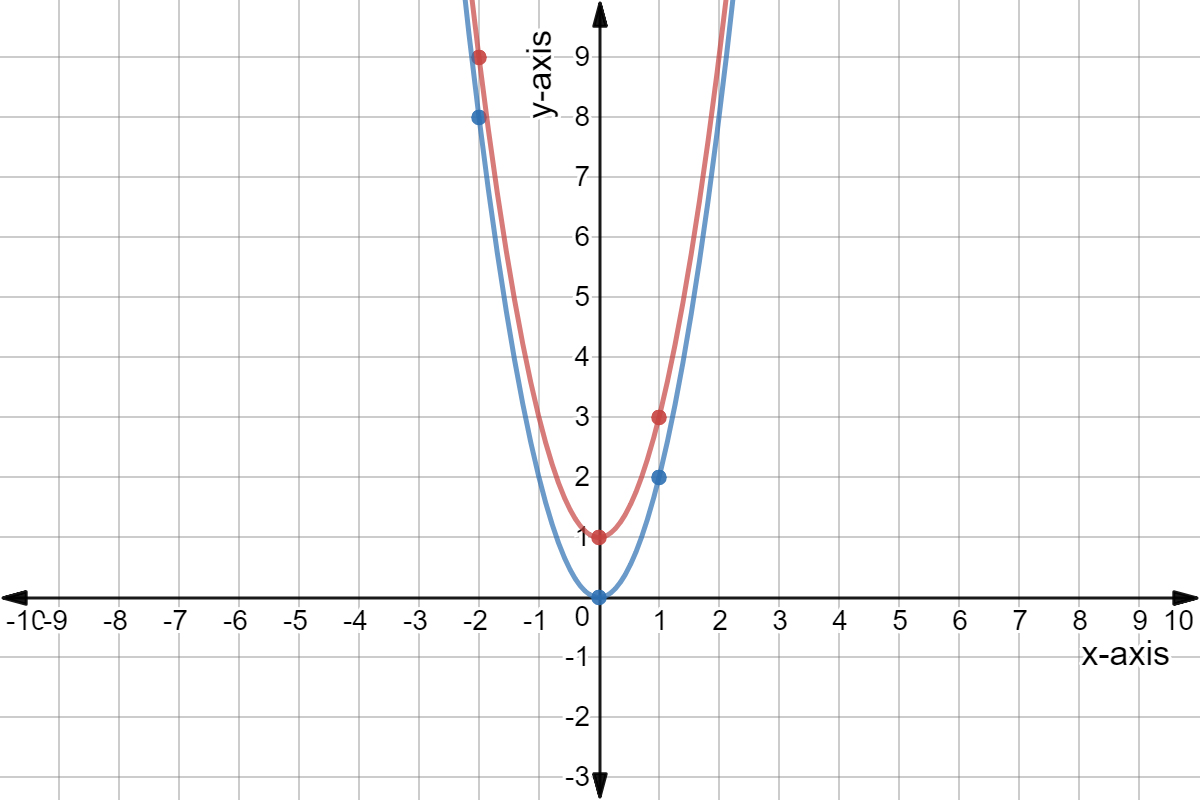
Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively




Graph The Parabola Y 2x 2 4x 1 Youtube
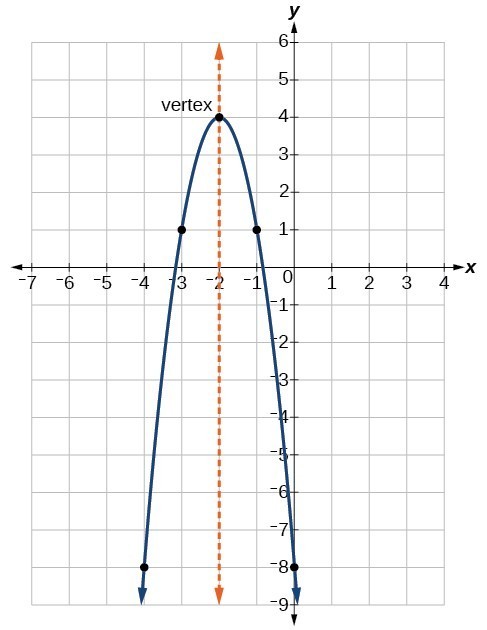



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic



Solution What Is The Graph Of Y 2x 2 2 Y Equals 2x Squared Plus 2



Solution Find The Vertex Of The Parabola Y 2x2 12x 13



How Do You Graph Y 2x 2 4x 3 Mathskey Com



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively




Quadratic Graph Example Y Ax Expii
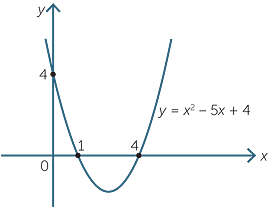



Quadratic Function



Untitled Document




6 The Graph Of The Parabola Given By The Function Y 2x2 2x 1 Opens Up Or Down Incorrect Your Answer Down Correct Answer Down Explanation The 2 In Y 2x2 2x 1




Content Transformations Of The Parabola



1




View Question The Parabolas Defined By The Equations Y 2x 2 4x 4 And Y X 2 2x 4 Intersect At Points A B And C D Where C Ge A What Is C A



Graph Y X 2 Youtube



Graphing Quadratic Functions




Transforming Graphs Of Functions




How To Draw Y 2 X 2



What S The Axis Of Symetry Vertex And Graph Y 2x 2 6x 1 Math Homework Answers



0 件のコメント:
コメントを投稿